圆方树

发表于 | 分类于 ， ，

emm，由方点和圆点组成的树。(命名鬼才)

前置芝士

仙人掌图

仙人掌图是一个无向连通图

仙人掌图上的任意边都至多存在于一个环里

为什么叫仙人掌图你自己画出来就知道了

基环树

emm,只有一个环的仙人掌,想看也可以去看看

进入正题

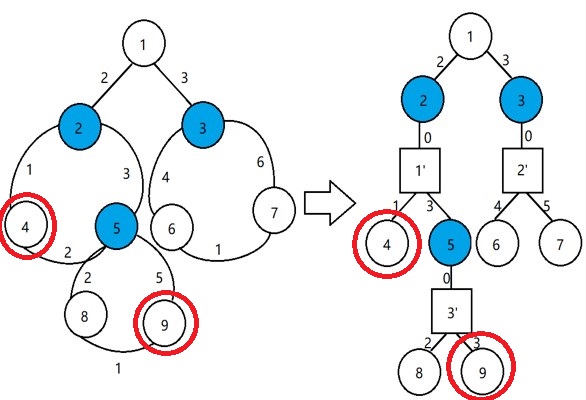
什么是圆♂方树?

圆方树就是一个用树来表达仙人掌的一种方式(方表示环,圆表示点)

对于一个环,我们定义一个根,作为从原图根(已指定)节点DFS下来遇到的第一个这个环上的节点

那么这个节点就是这个环在圆方树上的爸爸,而这个环上的其他节点则是这个环在树上的儿子

emm,就这样

怎么建圆♂方树?

well,观察一下:

—一个环就是一个联通分量

—一个联通分量里有且只有一个环

—每一个联通分量都是一个点双联通分量

很美妙的性质,似乎每一条性质都将我们引向一个毒瘤老爷子

但是这明显不是一个简单的tarjan(tbyangz:哪里不简单了)

—首我们仍按照正常tarjan跑,当我们找到了一个联通分量的时候,这就是个环了

—这个时候我们正处在的点,就是该环的环根了 (想想为什么)

—新建一个方点并把当前找到的联通分量中的所有点都与之连边(保留原编号)

—另外,如果搜到自己儿子与自己不在同一个联通分量中,就从自己向儿子连边(作圆方树边)

就酱

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
ll n,m,q,ff,tt,le,N,dfn[maxn],low[maxn],tot,h[maxn],cnt=1,H[maxn],Cnt;
struct Edge{ll from,to,next,len;}e[maxm],E[maxm];
void add(ll f,ll t,ll l){e[++cnt]={f,t,h[f],l};h[f]=cnt;}
void madd(ll f,ll t,ll l){add(f,t,l);add(t,f,l);}
void Add(ll f,ll t,ll l){E[++Cnt]={f,t,H[f],l};H[f]=Cnt;}
void Madd(ll f,ll t,ll l){Add(f,t,l);Add(t,f,l);}
stack<ll>st;ll V[maxn],Vtop,now_edge,len1[maxn],len2[maxn];
void Tarjan(ll u,ll pre_edge){
	dfn[u]=low[u]=++tot;ll v;
	for(int i=h[u];i;i=e[i].next){
		v=e[i].to;
		if(i==(pre_edge^1))continue;
		if(!dfn[v]){
			st.push(i);
			Tarjan(v,i);
			low[u]=Min(low[u],low[v]);
			if(low[v]>dfn[u])st.pop(),Madd(u,v,e[i].len);
			if(low[v]==dfn[u]){
				ll W=0;Vtop=0;
				while(1){
					now_edge=st.top();st.pop();
					W+=e[now_edge].len;
					V[++Vtop]=e[now_edge].from;
					len1[e[now_edge].from]=W;
					if(e[now_edge].from==u&&e[now_edge].to==v)break;
				}
				N++;
				for(int i=1;i<=Vtop;i++){
					len2[V[i]]=W-len1[V[i]];
					Madd(N,V[i],min(len1[V[i]],len2[V[i]]));
				}
			}
		}
		else if(dfn[v]<dfn[u]){st.push(i);low[u]=Min(low[u],dfn[v]);}
	}
}

其实确实挺简单的对吧

如何使用圆♂方树?

掌上最短(长)路

例题:luogu P5236-静态仙人掌

题目描述:

给你一个有nn个点和mm条边的仙人掌图，和qq组询问
每次询问两个点u,vu,v，求两点之间的最短路。

输入:

第一行三个正整数$n,m,q$意义如题目描述。
接下来$m$行，每行三个正整数$u,v,w$表示$u,v$之间有一条权值为$w$的无向边。
然后$q$行，每行两个正整数$u,v$询问$u$到$v$的最短路。

输出:

$q$行，每行一个正整数，对应一次询问的结果。

数据范围

$1≤n,q≤10000$
$1≤m≤20000$
$1≤w≤10^9$

思路分析:

暴力?

呵呵。

SPFA&Dijkstra?

$O(nm)$的时间,你要是i9-9900k的话你跑得过去我没话说,可惜你不是.(实测跑不过去)

还能怎么做?

冷静分析一波,这道题基本上时间要求$O(n log(m))$之类的神奇东西

然鹅,最短路能到$O(nlog(m))$的也就只有LCA了

不可做不可做

等等

仙人掌?

LCA?

圆方树啊!!!

:)

圆方树上LCA

其实说出来就没什么好讲的了

实际上有:

—DFS确定每个点的爸爸

—预处理计算出ST数组

—回答询问

还有一个神奇的坑点(实际不坑):

当两个点的LCA是方点时,你需要特判最后两个点的距离

For example:

pic 圆方树

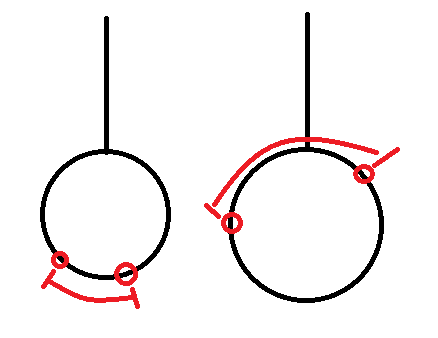
pic 掌上示意图

也就是两个换上的点之间的路径从上走还是从下走

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<bitset>
#include<vector>
#include<set>
#include<map>
#define ll long long
#define si short int
#define bl bool
#define maxn 30000
#define maxm 50000
#define inf 0x7fffffff
using namespace std;
ll Min(ll x,ll y){if(x<y)return x;return y;}
ll Max(ll x,ll y){if(x>y)return x;return y;}
ll read(){
	ll s=0,h=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')h=-1;c=getchar();}
	while(c>='0'&&c<='9'){s=s*10+c-'0';c=getchar();}
	return s*h;
}
void write(ll x){
	if(x>9){
		si tmp=x%10;
		write(x/10);
		putchar(tmp+'0');
	}
	else putchar(x+'0');
}
ll Pow(ll x,ll y,ll p){
	ll ans=1;
	while(y){
		if(y&1)ans=ans*x%p;
		x=x*x%p;y>>=1;
	}
	return ans;
}
ll n,m,q,ff,tt,le,N,dfn[maxn],low[maxn],tot,h[maxn],cnt=1,H[maxn],Cnt;
struct Edge{ll from,to,next,len;}e[maxm],E[maxm];
void add(ll f,ll t,ll l){e[++cnt]={f,t,h[f],l};h[f]=cnt;}
void madd(ll f,ll t,ll l){add(f,t,l);add(t,f,l);}
void Add(ll f,ll t,ll l){E[++Cnt]={f,t,H[f],l};H[f]=Cnt;}
void Madd(ll f,ll t,ll l){Add(f,t,l);Add(t,f,l);}
stack<ll>st;ll V[maxn],Vtop,now_edge,len1[maxn],len2[maxn];
void Tarjan(ll u,ll pre_edge){
	dfn[u]=low[u]=++tot;ll v;
	for(int i=h[u];i;i=e[i].next){
		v=e[i].to;
		if(i==(pre_edge^1))continue;
		if(!dfn[v]){
			st.push(i);
			Tarjan(v,i);
			low[u]=Min(low[u],low[v]);
			if(low[v]>dfn[u])st.pop(),Madd(u,v,e[i].len);
			if(low[v]==dfn[u]){
				ll W=0;Vtop=0;
				while(1){
					now_edge=st.top();st.pop();
					W+=e[now_edge].len;
					V[++Vtop]=e[now_edge].from;
					len1[e[now_edge].from]=W;
					if(e[now_edge].from==u&&e[now_edge].to==v)break;
				}
				N++;
				for(int i=1;i<=Vtop;i++){
					len2[V[i]]=W-len1[V[i]];
					Madd(N,V[i],min(len1[V[i]],len2[V[i]]));
				}
			}
		}
		else if(dfn[v]<dfn[u]){st.push(i);low[u]=Min(low[u],dfn[v]);}
	}
}
ll ST[maxn][21],dep[maxn],dis[maxn][21];
void Dfs(ll u,ll fa){
	ll v;ST[u][0]=fa;dep[u]=dep[fa]+1;
	for(int i=1;(1<<i)<=dep[u];i++){
		ST[u][i]=ST[ST[u][i-1]][i-1];
		dis[u][i]=dis[u][i-1]+dis[ST[u][i-1]][i-1];
	}
	for(int i=H[u];i;i=E[i].next){
		v=E[i].to;if(v==fa)continue;
		dis[v][0]=E[i].len;Dfs(v,u);
	}
}
ll que(ll x,ll y){
	ll ans=0,xx=x,yy=y;
	if(dep[x]<dep[y])swap(x,y);
	for(int i=17;i>=0;i--)
		if(dep[ST[x][i]]>=dep[y])
			ans+=dis[x][i],x=ST[x][i];
	if(x==y)return ans;
	for(int i=17;i>=0;i--)
		if(ST[x][i]!=ST[y][i]){
			ans+=dis[x][i]+dis[y][i];
			x=ST[x][i];y=ST[y][i];
		}
	if(ST[x][0]>n)return ans+Min(Min(len1[x]+len2[y],len1[y]+len2[x]),abs(len1[x]-len1[y]));
	ans+=dis[x][0]+dis[y][0];
	x=ST[x][0];y=ST[y][0];
	return ans;
}
int main(){
	N=n=read();m=read();q=read();
	for(int i=1;i<=m;i++){ff=read();tt=read();le=read();madd(ff,tt,le);}
	Tarjan(1,0);
	Dfs(1,0);
	for(int i=1;i<=q;i++)write(que(read(),read())),puts("");
	return 0;
}

码风略丑,别介意

掌上DP

例题:luogu P4410-无归岛

题目描述:

Neverland是个神奇的地方，它由一些岛屿环形排列组成，每个岛上都生活着之中与众不同的物种。

但是这些物种都有一个共同的生活习性：对于同一个岛上的任意两个生物，他们有且仅有一个公共朋友，即对同一岛上的任意两个生物a和b有且仅有一个生物c既是a的朋友也是b的朋友，当然某些岛上也可能会只有一个生物孤单地生活着。

这一习性有一个明显的好处，当两个生物发生矛盾的时候，他们可以请那个唯一的公共朋友来裁决谁对谁错。 另外，岛与岛之间也有交流，具体来说，每个岛都会挑选出一个最聪明的生物做代表，然后这个生物与他相邻的两个岛的代表成为朋友。

不幸运的是，A世界准备入侵Neverland，作为Neverland的守护者，Lostmonkey想知道在一种比较坏的情况下Never的战斗力。因为和朋友并肩作战，能力会得到提升，所以Lostmonkey想知道在不选出一对朋友的情况下Neverland的最大战斗力。即选出一些生物，且没有一对生物是朋友，并且要求它们的战斗力之和最大。

输入:

第一行包含用空格隔开的两个整数n和m，分别表示Neverland的生物种数和朋友对数。

接下来的m行描述所有朋友对，具体来说，每行包含用空格隔开的两个整数a和b，表示生物a和生物b是朋友（每对朋友只出现一次）。第m+2行包含用空格隔开的n个整数，其中第i个整数表示生物i的战斗力A.

输出:

仅包含一个整数，表示满足条件的最大战斗力.

数据范围:

输入数据保证$4≤n≤100000,1≤a,b≤n,1≤m≤200000,−1000≤Ai≤1000。$

思路分析:

算法分析:

实际上呢,这个就是一个带权最大独立集

SO->DP!!

问题来了,这DP个鬼啊,不是树啊啊啊

冷静,冷静

我们需要一棵树,但是仙人掌可以用圆方树转为树

欢乐地DP!!!

[pic 欢乐]

首先是状态:

我们肯定需要一维点对吧,但是一维明显很难维护所以我们就需要第二维->当前点取与不取

$ f[x][0/1]: $点x的子树中取$(1)$或不取$(0)$x时最大独立集的权值

然后是状态转移方程

那么对于原点:

而对于方点,我们还需要一个环上辅助DP:

这里我们分取环根与不取环根两种情况讨论,但他们的状态转移方程是一样的

这里将所有的环上节点存入了代表这个环的$vector$

所以这里的$i$是在枚举$vector$中元素时用的指针

而$v$则是$vector$中第$i$个元素代表的点的编号

So, that’s it!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<bitset>
#include<vector>
#include<set>
#include<map>
#define ll long long
#define ull unsigned long long
#define db double
#define ldb long db
#define si short int
#define bl bool
#define mem(a) memset(a,0,sizeof(a))
#define mee(a,b) memset(a,b,sizeof(a))
#define setnum(a,b,c) for(int kkk=1;i<=b;i++)a[kkk]=c[kkk];
#define setnums(a,b,c) for(int kkk=1;kkk<=b;kkk++)a[kkk]=c;
#define maxn 200005
#define maxm 500005
#define inf 0x7fffffff
#define r(a) a=read()
#define w(a) write(a);puts("")
#define W(a) write(a);printf(" ")
#define For(a,b,c) for(int a=b;a<=c;a++)
using namespace std;
ll Min(ll x,ll y){if(x<y)return x;return y;}
ll Max(ll x,ll y){if(x>y)return x;return y;}
ll read(){
	ll s=0,h=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')h=-1;c=getchar();}
	while(c>='0'&&c<='9'){s=s*10+c-'0';c=getchar();}
	return s*h;
}
void write(ll x){
	if(x>9){
		si tmp=x%10;
		write(x/10);
		putchar(tmp+'0');
	}
	else putchar(x+'0');
}
ll Pow(ll x,ll y,ll p){
	ll ans=1;
	while(y){
		if(y&1)ans=ans*x%p;
		x=x*x%p;y>>=1;
	}
	return ans;
}
ll n,m,f[maxn][2],g[maxn][2],ff,tt,le;
namespace cst{
	ll N,h[maxn],cnt=1,dfn[maxn],low[maxn],H[maxn],Cnt,tot,rf[maxn];
	vector<ll>ring[maxn];
	struct Edge{ll from,to,next,len;}e[maxm],E[maxm];
	void add(ll f,ll t,ll l){e[++cnt]={f,t,h[f],l};h[f]=cnt;}
	void madd(ll f,ll t,ll l){add(f,t,l);add(t,f,l);}
	void Add(ll f,ll t,ll l){E[++Cnt]={f,t,H[f],l};H[f]=Cnt;}
	void Madd(ll f,ll t,ll l){Add(f,t,l);Add(t,f,l);}
	stack<ll>st;ll V[maxn],Vtop,now_edge,len1[maxn],len2[maxn];
	void Tarjan(ll u,ll pre_edge){
		dfn[u]=low[u]=++tot;ll v;
		for(int i=h[u];i;i=e[i].next){
			v=e[i].to;
			if(i==(pre_edge^1))continue;
			if(!dfn[v]){
				st.push(i);
				Tarjan(v,i);
				low[u]=Min(low[u],low[v]);
				if(low[v]>dfn[u])st.pop(),Madd(u,v,e[i].len);
				if(low[v]==dfn[u]){
					ll W=0;Vtop=0;
					N++;rf[N]=u;
					while(1){
						now_edge=st.top();st.pop();
						W+=e[now_edge].len;
						V[++Vtop]=e[now_edge].to;
						len1[e[now_edge].to]=W;
						ring[N].push_back(e[now_edge].to);
						if(e[now_edge].from==u&&e[now_edge].to==v)break;
					}
					for(int i=1;i<=Vtop;i++){
						len2[V[i]]=W-len1[V[i]];
						Madd(N,V[i],min(len1[V[i]],len2[V[i]]));
					}
				}
			}
			else if(dfn[v]<dfn[u]){st.push(i);low[u]=Min(low[u],dfn[v]);}
		}
	}
}
using namespace cst;
void Rdp(ll u){
	//不选环根
	g[0][0]=f[ring[u][0]][0];
	g[0][1]=-inf;
	ll v;
	for(int i=1;i<ring[u].size();i++){
		v=ring[u][i];
		g[i][0]=f[v][0]+Max(g[i-1][0],g[i-1][1]);
		g[i][1]=f[v][1]+g[i-1][0];
	}
	f[ring[u][0]][0]=Max(g[ring[u].size()-1][0],g[ring[u].size()-1][1]);
	//选环根
	g[0][0]=-inf;
	g[0][1]=f[ring[u][0]][1];
	for(int i=1;i<ring[u].size();i++){
		v=ring[u][i];
		g[i][0]=f[v][0]+Max(g[i-1][0],g[i-1][1]);
		g[i][1]=f[v][1]+g[i-1][0];
	}
	f[ring[u][0]][1]=g[ring[u].size()-1][0];
}
void Tdp(ll u,ll fa){
	if(u<=n)f[u][1]=1;ll v;
	for(int i=H[u];i;i=E[i].next){
		v=E[i].to;if(v==fa)continue;
		Tdp(v,u);
		if(u<=n&&v<=n){
			f[u][0]+=Max(f[v][0],f[v][1]);
			f[u][1]+=f[v][0];
		}
	}
	if(u>n)Rdp(u);
}
int main(){
	n=read();m=read();
	for(int i=1;i<=m;i++){
		ff=read();tt=read();
		madd(ff,tt,1);
	}
	N=n;
	Tarjan(1,0);
	Tdp(1,0);
	cout<<Max(f[1][0],f[1][1])<<endl;
	return 0;
}

后话

这是这个博客的第一篇完整的题解

希望这个博客能够推动我的OI之路走的更远,更高!

(撒花)

日常推荐壁纸(我自己p的):[pic shiny mountain]

完